https://www.acmicpc.net/problem/2003
소스코드 사용 문제
투 포인터 알고리즘
1차원 배열에서 포인터를 2개를 이용하여 탐색하는 알고리즘.
한번에 2개의 포인터를 이용하기 때문에 그만큼 탐색이 빠르다(O(N))
투 포인터 알고리즘의 대표적인 문제는 위에서 언급한 문제와 같이 부분합을 구하는 문제이다.
부분합을 구하는 문제의 키포인트는
부분합이 구하고자 하는 값과 크거나 같으면 start(left) 인덱스를 +1 하고, 작으면 end(right) 인덱스를 -1 하는 것이다.
보통 부분합이라고 하면 누적합 알고리즘. 즉 Prefix Sum을 생각하기 쉽다.
그러나, Prefix Sum의 경우 특정 구간의 누적합을 구하는 케이스이고
투 포인터 알고리즘을 이용한 부분합 문제 풀이시에는
- 구간의 합이 M이 되는 경우
- 구간의 합이 최대가 되는 경우
- 구간의 합이 최소가 되는 경우
특정 구간의 정보를 계속해서 갱신해 나가며 체크해야 하는 경우에 사용한다.

시작은 start와 end가 같은 상태에서 시작하며 부분합을 0으로 두고 시작한다. 문제에서 요구하는 부분합은 5이므로 0<5 이기 때문에 end를 +1 해준다.

사진 설명을 입력하세요.
부분합 : 1 + 2 < 5 이므로 end + 1
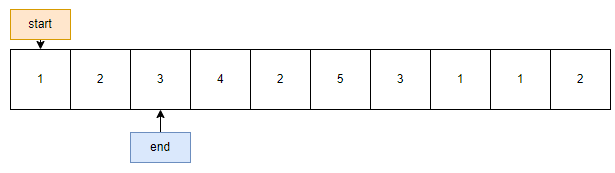
사진 설명을 입력하세요.
부분합이 1+2+3 >= 5 이므로 start를 +1 해주고 부분합에서 1을 빼준다.

사진 설명을 입력하세요.
부분합 : 2+3 = 5 이므로 count를 +1 하고 start를 + 1 해주고 부분합에서 2를 빼준다.

사진 설명을 입력하세요.
부분합 : 3<5 이므로 end를 +1 해준다. 이후는 앞과 같은 연산의 반복이다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <queue>
#include <deque>
#include <math.h>
#include <string>
#include <stack>
#include <set>
using namespace std;
int n,m;
int main(){
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
cin >> n >> m;
int arr[10001];
int left = 0;
int right = 0;
for(int i=0; i<n; i++){
cin >> arr[i];
}
int count = 0;
int sum = 0;
while(right <= n){
if(sum >= m){
sum -= arr[left];
left += 1;
}
else{
sum += arr[right];
right += 1;
}
if(sum == m){
count += 1;
}
}
cout << count << endl;
}투 포인터 알고리즘은 여러 형태로 사용할수 있다.
이분 탐색과 결합하여 사용할수도 있고, 슬라이싱 윈도우 기법을 이용해 면적을 구하는 데에도 사용할수 있다.
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [ALGORITHM] 최단경로 - 플로이드 워셜 (3) | 2024.12.31 |
|---|---|
| [ALGORITHM] 최단경로 - 다익스트라 (2) | 2024.12.24 |
| [ALGORITHM] 최대 연속 부분 구간 합 문제를 푸는 4가지 방법 (3) | 2024.12.16 |


