https://www.acmicpc.net/problem/1753
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;
int inf = 1e8+7;
int n,m;
int start;
vector<pair<int,int>> v[20001];
int dist[20001];
void dijkstra(int start){
for(int i=1; i<=n; i++){
dist[i] = inf;
}
dist[start] = 0;
priority_queue<pair<int,int>> q;
q.push(make_pair(0,start));
while(!q.empty()){
int now = q.top().second;
int now_dist = -q.top().first;
q.pop();
if(dist[now] < now_dist) continue;
for(int i=0; i<v[now].size(); i++){
int next = v[now][i].first;
int next_dist = v[now][i].second + now_dist;
if(dist[next] > next_dist){
dist[next] = next_dist;
q.push(make_pair(-next_dist,next));
}
}
}
}
int main(){
cin >> n >> m;
cin >> start;
for(int i=0; i<m; i++){
int a,b,c;
cin >> a>> b>> c;
v[a].push_back(make_pair(b,c));
}
dijkstra(start);
for(int i=1; i<=n; i++){
if(dist[i] == inf){
cout << "INF" << "\n";
}
else{
cout << dist[i] << "\n";
}
}
}
다익스트라 알고리즘
하나의 정점에 대해 다른 정점까지의 최단 경로를 구하는 알고리즘.
첫 정점을 기준으로 연결되어 있는 정점들을 추가해가며 최단 거리를 갱신하는 알고리즘
Distance 테이블과 Cost(Weight) 테이블을 따로 둔다.
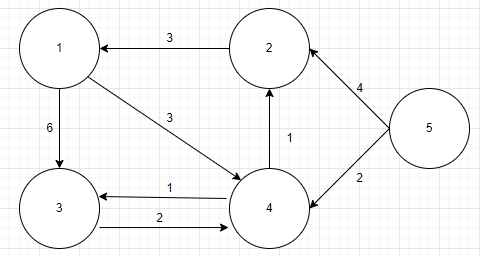
시작 노드를 5번 노드라고 가정을 하고 다익스트라 알고리즘을 수행해보자.
일단 모든 정점들을 큐에 넣는다.
|
i
|
d
|
p
|
|
5
|
0
|
/
|
|
1
|
inf
|
/
|
|
2
|
inf
|
/
|
|
3
|
inf
|
/
|
|
4
|
inf
|
/
|
|
5
|
4
|
3
|
2
|
1
|
|
0
|
INF
|
INF
|
INF
|
INF
|
방문하지 않은 노드들은 전부 INF로 표시한다.
시작점 5번 노드와 연결된 2번 ,4번 노드를 방문할 것인데, 통상적으로 우선순위는 노드번호가 작은 순서이다. 그러므로 2번 노드를 방문한다.
5번~2번노드의 최단거리는 5번노드까지의 최단거리 + 5~2와 현재 최단거리와의 최솟값이다
즉 dist[2] = min(dist[2], dist[5] + v[5][2]) 라는 뜻이다. (v는 그래프의 정보를 담은 테이블)
4번 노드도 위와 동일하게
dist[4] = min(dist[4], dist[5]+v[5][4]) 이다.
그리고 2번과 4번 모두 최솟값으로 갱신되었으므로 우선순위 큐에 push해준다.
그래서 갱신된 테이블을 보면
|
i
|
d
|
p
|
|
4
|
2
|
5
|
|
2
|
4
|
5
|
|
1
|
inf
|
/
|
|
2
|
inf
|
/
|
|
3
|
inf
|
/
|
|
4
|
inf
|
/
|
|
5
|
4
|
3
|
2
|
1
|
|
0
|
2
|
INF
|
4
|
INF
|
2번부터 방문했는데 왜 큐의 top에 4가 오는지는 큐가 우선순위큐이기 때문이다. dist를 기준으로 자동으로 정렬이 되어있는 큐이기 때문에 4가 앞으로 온다.
여기서 index가 4이고 dist[4]가 d보다 크거나 같으므로 연산을 시작한다. (dist[4]가 더 작으면 당연히 갱신하면 안된다.)
그래서 4를 pop하고 4 주변 노드들을 탐색한다.
dist[2] = min(dist[2], dist[4]+v[4][2])
dist[3] = min(dist[3],dist[4]+v[4][3])
여기서 dist[2]와 dist[3]이 갱신이 되기 때문에 큐에 또 넣어준다.
|
i
|
d
|
p
|
|
2
|
3
|
4
|
|
3
|
3
|
4
|
|
2
|
4
|
5
|
|
1
|
inf
|
/
|
|
2
|
inf
|
/
|
|
3
|
inf
|
/
|
|
4
|
inf
|
/
|
|
5
|
4
|
3
|
2
|
1
|
|
0
|
2
|
3
|
3
|
INF
|
다음 큐의 top의 인덱스가 2이므로 2번 노드를 간다.
dist[2] 는 3이고 큐에 저장된 d도 3이므로 pop후 연산을 시작한다. (다시 말하지만 dist[2]가 더 작았으면 pop후 그냥 넘어갔을 것이다)
2번 노드와 연결된 정점은 1이므로
dist[1] = min(dist[1], dist[1] + v[2][1]) 이다.
다음 테이블을 보면
|
i
|
d
|
p
|
|
3
|
3
|
4
|
|
2
|
4
|
5
|
|
1
|
6
|
2
|
|
1
|
inf
|
/
|
|
2
|
inf
|
/
|
|
3
|
inf
|
/
|
|
4
|
inf
|
/
|
|
5
|
4
|
3
|
2
|
1
|
|
0
|
2
|
3
|
3
|
6
|
큐의 top의 인덱스가 3이고 d가 3이므로
dist[3]과 비교해 같기 때문에 연산을 계속한다.
dist[4] = min(dist[4], dist[4]+v[3][4]) 이지만, 계산 값이 dist[4]가 더 작으므로 큐에 넣지 않는다.
|
i
|
d
|
p
|
|
2
|
4
|
5
|
|
1
|
6
|
2
|
|
1
|
inf
|
/
|
|
2
|
inf
|
/
|
|
3
|
inf
|
/
|
|
4
|
inf
|
/
|
|
5
|
4
|
3
|
2
|
1
|
|
0
|
2
|
3
|
3
|
6
|
이 경우
d는 4이고 dist[2]는 3이므로 dist[2]가 더 작아 연산하지 않는다.
|
i
|
d
|
p
|
|
1
|
6
|
2
|
|
1
|
inf
|
/
|
|
2
|
inf
|
/
|
|
3
|
inf
|
/
|
|
4
|
inf
|
/
|
|
5
|
4
|
3
|
2
|
1
|
|
0
|
2
|
3
|
3
|
6
|
이 경우에는 d는 6이고 dist[1]도 6이므로 연산을 하지만
4번 노드와 3번노드를 갱신하는 과정에서 연산값이 dist[4],dist[3]보다 크므로 큐에 넣지 않는다.
큐에 남은 모든값이 inf이므로 큐의 모든 값이 pop이 되고 반복문을 탈출하면서 위 테이블이 시작점 5번 노드부터 모든 정점까지의 최단거리이다.
만일 경로를 구해야 하는 경우라면 갱신시마다 map에다가 저장해주면 된다.
위에서 설명한 다익스트라 알고리즘은 개선된 다익스트라 알고리즘이지만, 개선되지 않은 다익스트라 알고리즘의 경우 우선순위큐에서 자동으로 진행했던 d가 최소인 값부터 탐색하는 과정을 직접 반복문을 통해 찾아내야하는 과정을 거친다. 이는 매우 비효율적이므로 쓰이지 않기 때문에 설명하지 않겠다.
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [ALGORITHM] 최단경로 - 플로이드 워셜 (3) | 2024.12.31 |
|---|---|
| [ALGORITHM] 최대 연속 부분 구간 합 문제를 푸는 4가지 방법 (3) | 2024.12.16 |
| [ALGORITHM] 투 포인터 (4) | 2024.12.07 |


