https://www.acmicpc.net/problem/11404
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <queue>
#include <deque>
#include <math.h>
#include <string>
#include <stack>
#include <set>
using namespace std;
long a,b;
int main(){
ios_base::sync_with_stdio(false); cin.tie(NULL);
int arr[101][101];
int n;
cin >> n;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
arr[i][j] = 123456789;
}
}
int m;
cin >> m;
while(m--){
int a,b,c;
cin >> a >> b >> c;
if(arr[a][b] > c){
arr[a][b] = c;
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
for(int k=1; k<=n; k++){
arr[j][k] = min(arr[j][k],arr[j][i]+arr[i][k]);
}
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(arr[i][j] != 123456789 && i!=j){
cout << arr[i][j] << " ";
}
else{
cout << 0 << " ";
}
}
cout << "\n";
}
}
플로이드 워셜 알고리즘
모든 노드에서 다른 노드까지의 최단 경로
다익스트라와 개념은 동일하게 단계별로 거쳐 가는 노드를 기준으로 알고리즘을 수행한다.
다익스트라와의 차이점
· 매 단계마다 방문하지 않은 노드 중에 최단 거리를 찾는 노드를 찾는 과정이 필요하지 않음
· 2차원 테이블에 최단 거리 정보를 그대로 저장함
· DP에 속함( 점화식을 이용하기 때문, 그러나 다익스트라도 엄밀히 메모이제이션을 이용한 DP)
· 각 단계마다 특정 노드 K를 거쳐 가는 경우를 확인함
Distanceab=min(Distanceab,Distanceak + Distancekb)
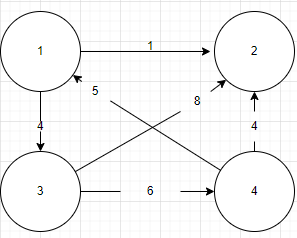
위와 같은 그래프에서
Distance12 는 노드 1에서 2로 바로 가는 경우도 있지만 3을 거쳐 가는 방법도 있다
즉,
Distance12 = min(Distance12,Distance13+Distance32) 인 것.
다른 노드들도 이와 같이 표현할수 있지만 더 큰 그래프를 그리는건 너무 어려우니 패스.
핵심은 한 노드에서 다른 노드까지 도착하는 cost를 구하는데에 있어서 direct한 경로가 최솟값이 아닐수도 있다는 것을 인지하고, 다른 노드를 거쳐서 가는 경로와 비교를 하는것이다.
그렇다면 꼭 다른 한 경로만 거쳐서 가야하는건가요? 라고 물어볼수 있는데
아니다. 여러 경로를 거쳐서 갈수 있다.
그러나 우리는 2차원 테이블을 dp 테이블, 즉 그 경로까지의 최솟값으로 저장해놓고 다루기 때문에 따로 그러한 경우는 다루지 않아도 된다. => 메모이제이션!
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [ALGORITHM] 최단경로 - 다익스트라 (2) | 2024.12.24 |
|---|---|
| [ALGORITHM] 최대 연속 부분 구간 합 문제를 푸는 4가지 방법 (3) | 2024.12.16 |
| [ALGORITHM] 투 포인터 (4) | 2024.12.07 |


